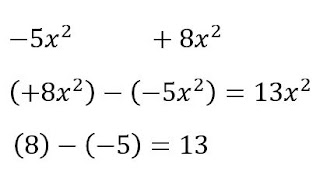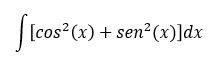Matemáticas básicas
Aquí encontrarás material sobre matemáticas.
miércoles, 10 de julio de 2019
viernes, 14 de septiembre de 2018
Razón de cambio: Cálculo Diferencial
La razón de cambio en cálculo es una velocidad. Es la velocidad con la que crece o disminuye la variable dependiente con respecto a la variable independiente. Generalmente sus unidades son desplazamiento/tiempo.
Existen dos razones de cambio, la razón promedio (velocidad promedio) y la razón instantánea (velocidad instantánea) La primera se da entre dos puntos, y la última en un solo punto.
A continuación veremos un ejemplo:
1. Calcular la razón promedio y la razón instantánea de la siguiente función.
Existen dos razones de cambio, la razón promedio (velocidad promedio) y la razón instantánea (velocidad instantánea) La primera se da entre dos puntos, y la última en un solo punto.
A continuación veremos un ejemplo:
1. Calcular la razón promedio y la razón instantánea de la siguiente función.
jueves, 21 de junio de 2018
Integrales de funciones trigonométricas: Cálculo Integral
Las integrales de funciones trigonométricas pueden ser directas o indirectas, es decir, en algunos casos tenemos que aplicar identidades trigonométricas para poder integrarlas.
El objetivo es transformar dicha función en una parecida a las reglas de integración ya existentes.
Todas la integrales están formadas o compuestas de la siguiente forma:
Algunas de las reglas de integración para las funciones trigonométricas (fórmulas) son las siguientes:
Como se puede observar, estás son integrales directas, pero se pueden generalizar cambiando "x" por "u" así "u" representa cualquier función. Esto será útil para el método de integración por sustitución.
Ahora veremos un ejemplo de integración indirecta, donde tendrémos que utilizar identidades trigonométricas para poder integrarlas.
Si tenemos la siguiente función, determinar su Antiderivada (integral)
Ejemplo:
Entonces cambiaremos el "uno menos coseno cuadrado de x" por " seno cuadrado de x" y quedará de la siguiente forma:
Ejemplo: Obtener la integral indefinida de la siguiente función

Como podemos observar son dos funciones que se están multiplicando, y no existe una regla de integración para la multiplicación, tampoco se ha visto una técnica para integrar a dos funciones que está multiplicando, por lo que tenemos que buscar otra alternativa, siendo que son funciones trigonométricas, debemos buscar en las identidades.
En las cuales encontramos la propiedad de angulo doble:

Entonces, sustituimos esta identidad en la integral, la cual queda de la siguiente forma:

Para integrar esta función utilizaremos la formula siguiente:

Donde U y dU son:

Ahora vemos que la integral no esta completa, porque du=2dx y en nuestra integral solo tenemos dx, nos hace falta el 2.
Por lo tanto lo tenemos que agregar de la siguiente forma para no alterar la ecuación, puesto que 2/2=1 y si multiplicamos por uno la ecuación tendremos exactamente lo mismo:

Luego dejamos el dos dentro de la integral y sacamos el medio, como se muestra a continuación:

Como ya está completo el integrando, ya podemos integrar la función.

Y luego simplificamos:

Este sería el resultado de la integración anterior, utilizando identidades trigonométricas.
El objetivo es transformar dicha función en una parecida a las reglas de integración ya existentes.
Todas la integrales están formadas o compuestas de la siguiente forma:
Como se puede observar, estás son integrales directas, pero se pueden generalizar cambiando "x" por "u" así "u" representa cualquier función. Esto será útil para el método de integración por sustitución.
Ahora veremos un ejemplo de integración indirecta, donde tendrémos que utilizar identidades trigonométricas para poder integrarlas.
Si tenemos la siguiente función, determinar su Antiderivada (integral)
Ejemplo:
Observamos que no existe ninguna regla de integración de esta forma, por lo tanto tenemos que transformarla en una parecida a las ya existentes.
Entonces tendremos que hacer uso de las identidades trigonométricas siguientes:
Entonces cambiaremos el "uno menos coseno cuadrado de x" por " seno cuadrado de x" y quedará de la siguiente forma:
Ahora haremos uso de la siguiente identidad:
Entonces nuestra integral quedaría de la siguiente forma.
Si observamos para esta integral sí existe una regla de integración y es la siguiente:
Por lo tanto la integral de:
Otra integral que a simple vista pareciera ser muy complicada, se puede hacer muy fácil aplicando las identidades. por ejemplo:
Pero si observamos, podemos hacer uso de la identidad:
Entonces nuestra integral se convierte en:
Ejemplo: Obtener la integral indefinida de la siguiente función
Como podemos observar son dos funciones que se están multiplicando, y no existe una regla de integración para la multiplicación, tampoco se ha visto una técnica para integrar a dos funciones que está multiplicando, por lo que tenemos que buscar otra alternativa, siendo que son funciones trigonométricas, debemos buscar en las identidades.
En las cuales encontramos la propiedad de angulo doble:
Entonces, sustituimos esta identidad en la integral, la cual queda de la siguiente forma:
Para integrar esta función utilizaremos la formula siguiente:
Donde U y dU son:
Ahora vemos que la integral no esta completa, porque du=2dx y en nuestra integral solo tenemos dx, nos hace falta el 2.
Por lo tanto lo tenemos que agregar de la siguiente forma para no alterar la ecuación, puesto que 2/2=1 y si multiplicamos por uno la ecuación tendremos exactamente lo mismo:
Luego dejamos el dos dentro de la integral y sacamos el medio, como se muestra a continuación:
Como ya está completo el integrando, ya podemos integrar la función.
Y luego simplificamos:
Este sería el resultado de la integración anterior, utilizando identidades trigonométricas.
Entonces, concluimos que, con las identidades trigonométricas podemos solucionar algunas integrales que parecen ser muy complicadas, transformándolas en integrales parecidas a la reglas de integración ya existentes.
miércoles, 13 de junio de 2018
La integral definida: Cálculo Integral
El teorema fundamental del calculo se define mediante la siguiente expresión matemática:







Esto quiere decir que: la integral de una función en un intervalo cerrado [a,b] es igual a la antiderivada de esa función evaluada con el límite superior menos la evaluación con el límite inferiror. Y este resultado representa el área bajo la curva descrita por dicha función.
Esta integral se resuleve de la misma forma que la integral indefinida, sin embargo a la antiderivada F(x) no se le agrega la constante de integración C. La única diferencia entre la indefinida y definida es que, al final tendremos que evaluar la antiderivada F(x) con los limites que nos dan: F(x)=F(b)-F(a)
Veamos un ejemplo:
Encontrar el valor de la integral definida de la siguiente función, en el intervalo [1,3]:
lo primero que tenemos que hacer, es expresarlo en forma de integral definida:
y si lo graficamos lo veríamos de la siguiente forma:
con sus límites superior e inferior.
1. resolvemos la integral como si fuese una indefinida
2. Nos quedamos con la antiderivada que obtuvimos, sin incluir a la constante de integración C.
3. ahora tendremos que evaluar a esta función, primeramente con el limite superior 3 y restarle la evaluación de la función con el límite inferior 1. es decir entre el intervalo [1,3]
la primera evaluación F(3)=165/4 y F(1)=119/12
por lo tanto recordemos que F(x)=F(b)-F(a), entonces
F(x)=F(3)-F(1) F(x)=165/4 - 119/12 F(x)=94/3 F(x)=31.3333
Entonces el valor de la integral indefinida de la función en el intervalo [1,3] es de:
F(x)=31.3333
La integral definida también es conocida como el área bajo la curva, como se muestra en la figura. El área sombreada de azul, sería el área bajo la curva limitada por el intervalo [a,b]
Cuando un área está sobre el eje x, se dice que es positiva y cuando está por debajo se dice que es negativa y se debe convertir en positiva para poder encontrar su valor, ya que un área nunca debe ser negativa. Para convertir un área negativa a positiva se debe multiplicar por (-1) o agregar el signo (-) antes de la integral que representa esta área.
Ejemplo:
En la imagen anterior observamos que hay dos áreas, una sobre el eje "x" y la otra bajo este. Necesitamos saber el área total sombreada de azul, por lo que tenemos que integrar la función en todo el intervalo, pero si integramos de una sola vez, las áreas se van a restar en vez de sumarse, puesto que una es positiva y otra negativa.
Entonces ¿Que debemos hacer? Bueno, primeramente tendremos que dividir la integral general en el numero de áreas que hay, es decir en dos. y los intervalos también se dividirán. Para esto tendremos que encontrar el valor de "x" donde la gráfica intersecta (cruza) al eje x.
Para esto, se iguala la función de la gráfica a cero y se resuelve, puesto que el máximo exponente de x es 3, debe tener 3 soluciones.
Resolvemos la ecuación y los siguientes valores son las soluciones.
x=0.91909 x=-1.13781 x=-4.78128
Si observamos, el intervalo de integración es de [0,2] entonces vamos a tomar los valores de la solución que estén dentro de este intervalo, es decir el primer valor de x=0.91909
Entonces, los nuevos intervalos serán: [0,0.91909] y [0.91909,2]
Como son dos áreas, el intervalo se divide en dos al igual que la integral, además la segunda área es negativa por lo que tenemos que agregar un signo (-) a la segunda integral:
Luego hacemos las evaluaciones correspondientes a cada limite:
después sustituimos
Entonces, realizaremos los cálculos y obtendremos que el área total de las dos áreas sombreadas es: 13.57 unidades cuadradas.
Ejemplo: Determinar el valor de la integral definida de la siguiente función
Paso 1: debemos integrarla y luego indicar que la evaluaremos con los limites dados.
la anterior imagen muestra la integral de esa función y está indicado que se evaluará desde -1 hasta 3.
Paso 2: sustituir los limites, inferior y superior, recordemos que el superior va primero.
Después procederemos a resolver las operaciones que están dentro de los paréntesis.
Dando como resultado lo anterior, el valor de la integral definida solicitada es: 85.333 unidades cuadradas.
Suscribirse a:
Comentarios (Atom)
Suma y resta de terminos semejantes.
Antes de ver que son los términos semejantes vamos a ver ¿qué es un término? Un término está compuesto por el signo, el coeficiente, la...

-
La ley de enfriamiento de Newton describe la forma en que se comporta un cuerpo con temperatura To expuesta a una temperatura ambiente o c...
-
El teorema fundamental del calculo se define mediante la siguiente expresión matemática: Esto quiere decir que: la integral de una fun...
-
Antes de ver que son los términos semejantes vamos a ver ¿qué es un término? Un término está compuesto por el signo, el coeficiente, la...