El objetivo es transformar dicha función en una parecida a las reglas de integración ya existentes.
Todas la integrales están formadas o compuestas de la siguiente forma:
Como se puede observar, estás son integrales directas, pero se pueden generalizar cambiando "x" por "u" así "u" representa cualquier función. Esto será útil para el método de integración por sustitución.
Ahora veremos un ejemplo de integración indirecta, donde tendrémos que utilizar identidades trigonométricas para poder integrarlas.
Si tenemos la siguiente función, determinar su Antiderivada (integral)
Ejemplo:
Observamos que no existe ninguna regla de integración de esta forma, por lo tanto tenemos que transformarla en una parecida a las ya existentes.
Entonces tendremos que hacer uso de las identidades trigonométricas siguientes:
Entonces cambiaremos el "uno menos coseno cuadrado de x" por " seno cuadrado de x" y quedará de la siguiente forma:
Ahora haremos uso de la siguiente identidad:
Entonces nuestra integral quedaría de la siguiente forma.
Si observamos para esta integral sí existe una regla de integración y es la siguiente:
Por lo tanto la integral de:
Otra integral que a simple vista pareciera ser muy complicada, se puede hacer muy fácil aplicando las identidades. por ejemplo:
Pero si observamos, podemos hacer uso de la identidad:
Entonces nuestra integral se convierte en:
Ejemplo: Obtener la integral indefinida de la siguiente función
Como podemos observar son dos funciones que se están multiplicando, y no existe una regla de integración para la multiplicación, tampoco se ha visto una técnica para integrar a dos funciones que está multiplicando, por lo que tenemos que buscar otra alternativa, siendo que son funciones trigonométricas, debemos buscar en las identidades.
En las cuales encontramos la propiedad de angulo doble:
Entonces, sustituimos esta identidad en la integral, la cual queda de la siguiente forma:
Para integrar esta función utilizaremos la formula siguiente:
Donde U y dU son:
Ahora vemos que la integral no esta completa, porque du=2dx y en nuestra integral solo tenemos dx, nos hace falta el 2.
Por lo tanto lo tenemos que agregar de la siguiente forma para no alterar la ecuación, puesto que 2/2=1 y si multiplicamos por uno la ecuación tendremos exactamente lo mismo:
Luego dejamos el dos dentro de la integral y sacamos el medio, como se muestra a continuación:
Como ya está completo el integrando, ya podemos integrar la función.
Y luego simplificamos:
Este sería el resultado de la integración anterior, utilizando identidades trigonométricas.
Entonces, concluimos que, con las identidades trigonométricas podemos solucionar algunas integrales que parecen ser muy complicadas, transformándolas en integrales parecidas a la reglas de integración ya existentes.









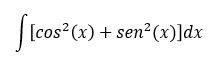





No hay comentarios:
Publicar un comentario